Accurately predicting emergent properties of fluids

A key interest of the Cox Group is to understand — armed only with knowledge of the interactions between particles — what properties emerge on large length scales. This is especially challenging when characteristic length scales of microscopic correlations compete with the geometry imposed on the system — a prominent example is confinement in nanoporous media.

We have recently developed a first-principles theory of electromechanics in fluids rooted in hyper-density functional theory. Using machine learning methods, we can use this theory to investigate polar fluids such as water — we recently discovered a new phenomenon we dub “dielectrocapillarity”, which describes how electric field gradients influence adsorption into porous materials. These results build on a significant development from our group concerning how to accurately account for nonlocal correlations arising from electrostatic interactions.

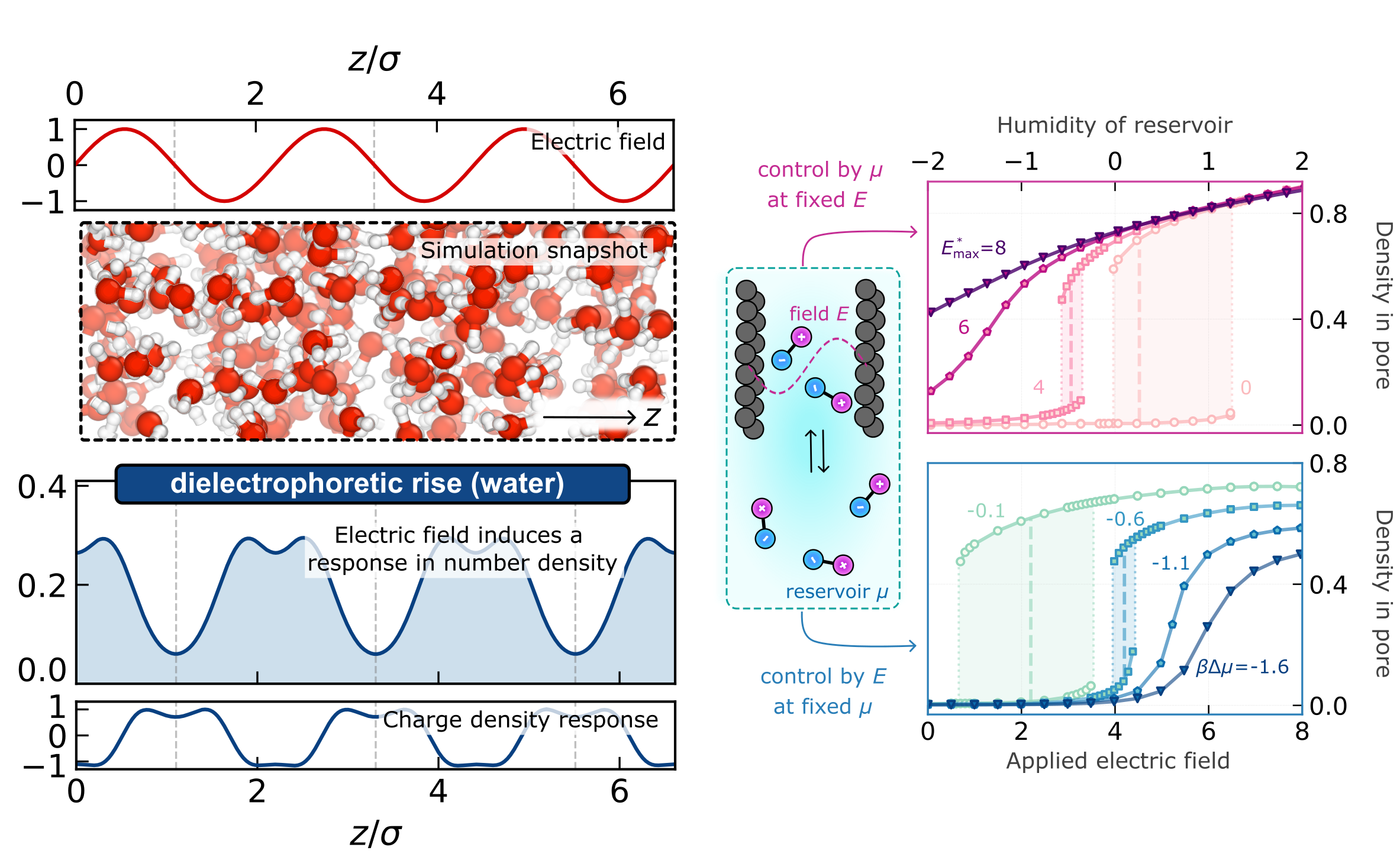
Left: Applying an electric field to bulk water induces a response in the number density — a perfect example of electromechanics! Right: Electric fields can also be used to control adsorption into pores. In the top panel, turning on a field makes it easier for the fluid to enter the pore. In the bottom panel, we see that the electric field can act as a switch between empty and filled states.

Crystals in solution: Surface structure and morphology

Our research also extends beyond the behavior of liquids to explore how the surrounding fluid environment influences solid surfaces. In particular, we are interested in polar crystal surfaces and in modelling crystal growth from microscopic principles.

Understanding these processes is key to controlling crystal morphology and interfacial structure — insights that are crucial for applications ranging from energy storage materials, biomineralization, and catalysis.

We have shown how the aqueous environment can stabilise the polar surface of AgI, and the impact this has on its ice-nucleating capability. We also demonstrated how to effectively simulate macroscopic polar crystal surfaces, and we established a theory for the stabilization of polar surfaces in solution.